Bridge over troubled water
The Problem
Constraints:
- Reduce the number of popsicle sticks(ie. cost)
- Must fit within 22"x6" frame
Considerations:
- Sticks are not uniform
Design a truss which can support
200lb using only:
- popsicle sticks
- wooden gusset plates
- wood glue
Statistical Analysis of Data & Calculations for Structural Safety
Popsicle stick average force: 9.469 lb
Popsicle stick standard deviation: 2.56 lb
b = 0.368 in
d = 0.07 in
M = PL/4 = (9.469 lbs * 2.56 in)/4 = 6.06 lb in
S = bd^2/ 6 = (0.368 * 0.07^2)/6 in^3 = 0.000301
Mstddev = PL/4 = (2.56 lbs * 2.56 in)/4 = 1.638 in
Sstddev = bd^2/6 = 0.000301
Bending stress = M/S = 20164 psi
20164 psi *bd = 519.429 lb (max bar force)
Bending stress stddev = 544 psi
544 psi * bd = 14.01 lb
Force average: 519.429lb
Force standard deviation: 14.01 lb
To have an error less than 5%:
Area under standard normal curve fromZ = -1.7
Z = (x - average)/(standard deviation)
x = 495.612 lb=max bar force
Material testing data summary
The solution
Designs considered
- Howe Truss with 6 splices and 12 joints
- 157.6"
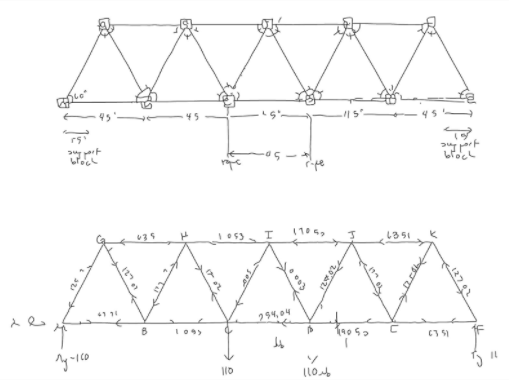
- Warren Truss with no splices and 11 joints
- 118.5"
- Variation on Warren Truss with no splices
- 88.65"
- King Post Truss with 8 splices and 4 joints
- 52.62"
Warren Truss with no splices
2nd smallest bar length
All bar forces were safely under the 5% fail rate
Required no splices(less room for human error)
Easiest to construct without errors
Outcome:
Our truss, once built, was able to support Professor Kelvin’s weight as he walked the plank up until he was three feet away. When Kelvin was around four feet away our truss started creaking. At three feet away, the truss broke. It broke on the top middle joint due to compression forces.
Although we chose this design because of its simplicity in construction, we ended up being a little to relaxed and found our truss to be slightly too long to fit. It was remedied the day of testing by sanding off the ends.